The probables in the Potential Future use Bayesian hooks into the events of Now to continuously form Reality
We continue discussing the Time Path, with a closer look at what must be happening when potential events become real events. We examine the natural flow of probable uncertainties that seem to be at play. In a sense, we try to “clarify” by emphasizing probability, a topic most people find hard to visualize.
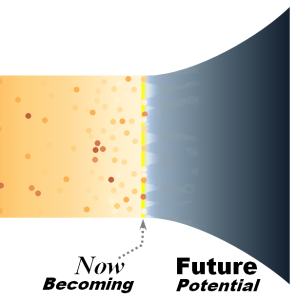
Fig 1 is a visualization image meant to focus the discussion on the structure of time. Activity flows like this ← from right to left in the image. Click any image for full resolution
- the Future is an undetermined swirl of potential actions converging toward events. Probability is the only reality.
- the Now is the focus of where things happen. Now is the coalescence of probabilities into actualized events or vanished alternatives, the occurrence point where things possible become things actual.
- the Past is the record of actual events that have happened. Happening events push realized ones out of the becoming Now and into the actualized past.
The Time Path is a speculative view, developed from my own and many other viewpoints. This is a post in the Time Path Ontology chain. I suspect that you should read the previous Time Path posts to get the full visualization. I am solely responsible for any errors or misstatements.
Is time really like the flight of an arrow?
It certainly feels like we are rushing forwards toward something in the future. Really? Why not backwards into the past, instead? This is a reasonable question if events truly are “flowing toward the future,” because basic physics allows actions to work equally well forwards or backwards. We grew up with the imagery of flowing time that it is hard to discard.
The picture we present is of possible actions converging to the events that form reality. This occurs in the happening time of Now. After this convergence, there is nothing more to be done because the events exist and are part of the record. In other words, we humans are not flowing on the stream of time, we are experiencing. Right Now, reality forms around us. One way or another, the entire universe changes in the Now.
The Conditional Connection.
The Time Path view pictures the future as undetermined possible actions that either coalesce to real events as their associated probabilities change to one (1), or that evaporate away as the associated probabilities become null (0).
How do random probabilities of all kinds of events “know” to converge into a real event? This is our main issue, and it must involve conditional probabilities, sometimes called Bayesian.
Conditional probability is formed when
- a potential activity (call it Q) has some probability of resolving into the event Q,
- but if an event P emerges prior to the Q event, the existence of P can change how the potential Q solidifies into event Q.
Example Mayoral candidate Quincy may enter an election contest with a 40% probability for winning, but he doesn’t have enough campaign cash to even send out a mailing. He has a remote connection to a possible supporter, Peterson, who has donated generously to other campaigns. If wealthy Peterson would donate sufficient money, Quincy’s chance to win could shift to 80% prior to the election. Donor Peterson’s cash is a prior condition to candidate Quincy’s election. If the prior donation is early enough and high enough, election day chance might reach 100%. Mayor Quincy happens.
The happening set of events generate prior information that feeds into the probability of the converging Q‘s properties.
Priors Such prior information are the conditions that force related probabilities to change. Sometimes referred to as priors.
Our example The Peterson donation is the prior that would allow potential mayor Quincy to coalesce into actual mayor Quincy.
Bayesian probability is the extension of Conditional Probability to account for multiple prior conditions. Multiple priors can mutually interact to bring in truly unexpected results – spookily weird. Even professional mathematicians, experts in statistics, can be confused.
We are staying far away from the math behind probability, and this is especially true as we take on Bayes’ Theorem. As we said in Physics – Science or Ideology, correct math is the automatic logic that gets us to the correct solution, but “math is hard” unless you have mastered every step leading up to your problem. Even after the issue has been mathematically resolved, it is not necessarily clear what those steps meant to us who live in the real world.
Let’s Make A Deal It is easy to demonstrate Bayesian changes.
Box 1 shows a short simplification that captures what is meant by the Monty Hall problem. This TV show has run off and on for 48 years and is famous for its demonstration that most people do not understand probability.
Read about this on line, or in Jason Rosenhouse wonderful book, The Monty Hall Problem .
Choose a door then Monty opens one. This problem has 2 priors • Monty Hall never opens the door you select • Monty Hall never opens the door with the prize (he knows the prize door).
In 1991 Marilyn vos Savant (one of the highest IQ ratings in world) responded to a question in a popular Sunday magazine column. Change your choice, said she, and you double your chance of winning.
Outrageous! Nothing happened to the basic situation behind the door you chose or the other door. Your starting probability was one chance in three for any door; that could not change! Ms. vos Savant received over ten thousand irate and insulting letters, more than a thousand from math professors who were abusive. Even famous mathematician Paul Erdös became irate!
But she was right.
Later, National Public Radio opened a website that let people play the game on a computer, 3 choices: (A) Choose one of 3 doors, open it. (B) Get the Monty Hall deal, do not switch doors. (C) Get Monty Hall deal, switch. Even 5th grade classes demonstrated the truth of Ms. vos Savant’s analysis.
Another Bayesian example A lie detector shows positive and it can detect lies 98.5% of the time! The suspect pleads innocent but fails the detector. We are more than 98% sure suspect lying, right? No, not really. Priors • 23% of all subjects tested are so nervous that they fail the detector, and • only 1.3% percent of the population would do what the suspect is accused of. Bayes’ Theorem says that the test has a 5.4% of being correct, not the 98.8% from tests with known lies and truths. The priors forced the probabilities to change.
Priors modify probability in ways that can be shockingly big and unbelievably subtle. Solutions to our Bayesian examples are in this PDF here.
Priors are a big reason for the huge disconnect between
the perception of chance and its reality.
How could potential actions coalesce into real events?
Bayesian priors are the linkages, the hooks, that ensure the smooth convergence of unrealized possibles into actualized events.
Example to show effects of priors (hypothetical control of a deer herd)
Reports of a deer herd living in the City have led to calls for a cull. Advocates say that lack of predators cause the herd to grow without limit, opponents say flower gardens in a few rich households are being bothered and no one should consider a deer kill.
- Advocates say home vegetable gardens exist in all income ranges, the deer are experiencing heavy growth, and native vegetation is being eradicated in all City parks.
This report forms a positive Bayesian prior and raises a cull’s probability.
- Opponents say that sterilization would work, and the beautiful, graceful deer would still grace our City.
This report forms a negative Bayesian prior and lowers a cull’s probability.
- Advocates point out that sterilization is invasive and dangerous to does and leaves the deer to continue (a) destroying plant diversity and (b) adding to continued danger of deer/vehicle collisions (positive prior for probability).
- Opponents suggest birth control as a non surgical technique, non invasive and is being tested elsewhere (negative prior).
- TV news reports a pet dog dies by sharp deer hooves while trying to drive the doe off the property.
- Opponents say … Advocates respond …
… On and on, each side sharpens the probability of the City Council’s decision. After much sharpening of the probability by the priors, realization happens when the the Council debates and votes. The cull either occurs (1, certainty) or does not (0, null).
Back To The Bayesian Future. Our example used a sequence of single priors, easy to follow, although like any probability, not easy to predict. But the future is the a halo of mutually associated potential actions surrounding every possibility. All actualized events close to Now link to the unrealized possibles as Bayesian priors, changing the overall probability of the event so that it evaporates when it becomes null, or actualizes when it becomes certain.
For discussion purposes, pick one potential activity and call it the futureEvent , call its coalesced form the actualEvent.
- All is Future, nothing is actualized. Every futureEvent has an associated array of probabilities to detail of its exact structure were it to converge into Now.
- All is Future, nothing is actualized. Every futureEvent has a halo of associated potential activities that link to one or more of the futureEvent‘s details through potential Bayesian processes.
- The priors begin to actualize. These associated possibilities begin convergence toward either one (1) and is actualized, or null (0) and vanish from possibility.
- The actualEvent forms. The newly realized events are prior information, they connect to the given unrealized futureEvent and modify its probability structure, later emerging priors make further changes. The futureEvent‘s total probability ultimately coalesces to certainty so that the actualEvent appears Now. (We followed an action that actually did turn into an event.)

Fig 2 Events that emerge from Now are Bayesian prior information to future possibles. The dotted lines indicate connection to the priors. Image (c) 2015 LastTechAge .
Fig 2 is a visualization of the Time path close to Now, the yellow/white divider. Possible actions (right) are actualized (Now) into events (left). Events move toward the left and fade into the fog of the past.
The halo of all future possibilities are shown by the gray fog. To visualize this, we use a small subset of future possibilities and near past events and show the depletion of a possible’s probability which vanishes, and the coalescence of possibles into actuals.
The continuously appearing events become Bayesian priors that help adjust the probability for each Future potential action toward actualization or nullification. Fig 2 visualizes these links as dotted lines from real events to probable potential actions.
Now picture the entire future as an amorphous cloud of all possible actions that are adjusted by the panoply of events that continuously emerge Now. This is a network of mutually interacting probabilities, the true complexity in our universe.
Describing the becoming of Now
One of our problems in making a physical model is that probability is a form of information that applies to not-yet actions; it is not a physical property of a fully formed Event. But all events in our reality has probability whose value is exactly unity (1) and we ought to be able to make the extensions along the timepath.
Another issue is how to describe something that is not part of time or space? You need to be outside our 4 dimensional universe to discuss it, and right now this is in the human realm of pure logic. Werner Heisenberg (quantum mechanics fame) said that underneath everything was probability and logic, and nothing else – a concept that causes its own instinctual rejection by most people. Could Heisenberg have had something like our Time Path view in mind?
……………………………….
Charles J. Armentrout, Ann Arbor
2015 Aug 11
Listed under General… a post in the thread General > Time Path
Have a comment? Click on the title of this post, go to bottom, let us know.
Related posts: Click the INDEX menu under the Banner picture